如图所示,在y>0的区域内有沿y轴正方向的匀强电场,在y<0的区域内有垂直坐标平面向里的匀强磁场.一电子(质量为m、电量为e)从y轴上A点以沿x轴正方向的初速度v0开始运动.当电子第一次穿越x轴时,恰好到达C点;当电子第二次穿越x轴时,恰好到达坐标原点;当电子第三次穿越x轴时,恰好到达D点.C、D两点均未在图中标出.已知A、C点到坐标原点的距离分别为d、2d.不计电子的重力.求:(1)电场强度E的大小;
(2)磁感应强度B的大小;
(3)电子从A运动到D经历的时间t.

电子的运动轨迹如图所示
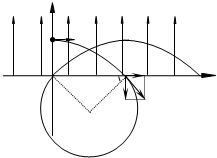
(1)电子在电场中做类平抛运动,设电子从A到C的时间为t1,
则 2d=v0t1
d=
a1 2 t 21
a=eE m
解得 E=m v 20 2ed
(2)设电子进入磁场时速度为v,v与x轴的夹角为θ,则 tanθ=
=1,得θ=45° at1 v0
解得 v=
v02
电子进入磁场后做匀速圆周运动,洛仑兹力提供向心力,得 evB=mv2 r
由图可知 r=
d2
解得 B=mv0 ed
(3)由抛物线的对称关系,电子在电场中运动的时间为 3t1=6d v0
电子在磁场中运动的时间 t2=
T=3 4 3 4
=2πm eB 3πd 2v0
电子从A运动到D的时间 t=3t1+t2=3d(4+π) 2v0
答:
(1)电场强度E的大小为
.m v 20 2ed
(2)磁感应强度B的大小为
;mv0 ed
(3)电子从A运动到D经历的时间t为
.3d(4+π) 2v0
