如图甲所示,竖直放置的金属板A、B中间开有小孔,小孔的连线沿水平放置的金属板C、D的中间线,粒子源P可以间断地产生质量为m、电荷量为q的带正电粒子(初速不计),粒子在A、B间被加速后,再进入金属板C、D间偏转并均能从此电场中射出.已知金属板A、B间的电压UAB=U0,金属板C、D长度为L,间距d=.两板之间的电压UCD随时间t变化的图象如图乙所示.在金属板C、D右侧有二个垂直纸面向里的均匀磁场分布在图示的半环形带中,该环带的内、外圆心与金属板C、D的中心O点重合,内圆半径Rl=,磁感应强度B0=.已知粒子在偏转电场中运动的时间远小于电场变化的周期(电场变化的周期T未知),粒子重力不计.
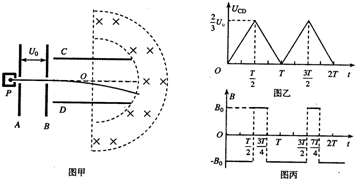
(1)求粒子离开偏转电场时,在垂直于板面方向偏移的最大距离;
(2)若所有粒子均不能从环形磁场的右侧穿出,求环带磁场的最小宽度;
(3)若原磁场无外侧半圆形边界且磁感应强度B按如图丙所示的规律变化,设垂直纸面向里的磁场方向为正方向.t=时刻进入偏转电场的带电微粒离开电场后进入磁场,t=时该微粒的速度方向恰好竖直向上,求该粒子在磁场中运动的时间为多少?
(1)设粒子进入偏转电场瞬间的速度为v0,
对粒子加速过程由动能定理得qU0=mv02-0,
进入偏转电场后,加速度a=,
设运动时间为t,则有L=v0t,
只有t=时刻进入偏转电场的粒子,垂直于极板方向偏移的距离最大
y=at2=L;
(2)t=时刻进入偏转电场的粒子刚好不能穿出磁场时的环带宽度为磁场的最小宽度.
设粒子进入磁场时的速度为v,y=L=×d=d,Uy=y=U0,
对粒子的偏转过程,由动能定理得:qU0=mv2-mv02,解得:v=;
在磁场中做圆周运动的半径为R==;
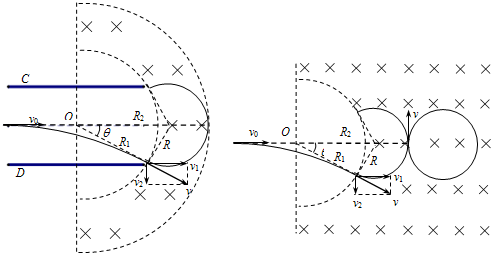
如图所示,设环带外圆半径为R2,由数学知识可得:(R2-R)2=R12+R2,解得R2=L;
所求d=R2-R1=(1-)L;
(3)微粒运动轨迹如图所示,
微粒在磁场中做匀速圆周运动的周期为T1=,
设粒子离开电场时偏转角为θ,则tanθ=,解得:θ=30°,
由几何关系可知微粒运动时间轨迹对应的圆心角为:φ=120°,
此过程微粒运动的时间为t=,
由图可知微粒在磁场中运动的时间:
t′=+T1+=T1==;
答:(1)粒子离开偏转电场时,在垂直于板面方向偏移的最大距离是L;
(2)若所有粒子均不能从环形磁场的右侧穿出,环带磁场的最小宽度是(1-)L;
(3)该粒子在磁场中运动的时间为.


