如图甲所示,偏转电场的两个平行极板水平放置,板长L=0.08m,板距足够大,两板的右侧有水平宽度l=0.06m、竖直宽度足够大的有界匀强磁场.一个比荷为q/m=5×107 C/kg的粒子(其重力不计)以v0=80m/s速度从两板中间沿与板平行的方向射入偏转电场,进入偏转电场时,偏转电场的场强恰好按图乙开始随时间发生变化,粒子离开偏转电场后进入匀强磁场,最终垂直右边界射出.求:
(1)粒子在磁场中运动的速率v;
(2)粒子在磁场中运动的轨道半径R;
(3)磁场的磁感应强度B;
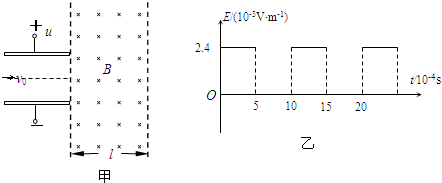
(1)电子在偏转电场中的运动时间
t=
=l v0
s=1.00×10-3 s ①0.08 80
对比乙图,电子在极板间的时间是偏转电压的一个周期
第一个t=5.00×10-4 s内,电子做类平抛运动,则有
v⊥=
t═60 m/s ②qE m
故v=
=
+v 20 v 2⊥
m/s=1.0×102 m/s ③802+602
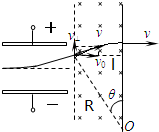
(2)电子在磁场中的轨迹如图所示.由题粒子进入匀强磁场,最终垂直右边界射出,由几何知识得知,粒子在磁场中的偏向角等于在电场中的偏向角,设此偏向角为θ.
设电子在磁场中做圆周运动的半径为R.
电子离开电场时,有 sinθ=v⊥ v
在磁场中,有sinθ=l R
∴
=l R
④v⊥ v
得 R=
l=v v⊥
×0.06m=0.1 m ⑤100 60
(3)粒子在磁场中做匀速圆周运动,有 qvB=m
⑥v2 R
得B=
=mv qR
T=2.0×10-5 T ⑦100 5×107×0.1
答:
(1)粒子在磁场中运动的速率v是1.0×102 m/s;
(2)粒子在磁场中运动的轨道半径R是0.1m;
(3)磁场的磁感应强度B是2.0×10-5 T.
