问题
问答题
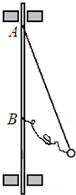
如图所示,一个质量为m的小球由两根细绳拴在竖直转轴上的A、B两处,AB间距为L,A处绳长为
L,B处绳长为L,两根绳能承受的最大拉力均为2mg,转轴带动小球转动.则:2
(1)当B处绳子刚好被拉直时,小球的线速度v多大?
(2)为不拉断细绳,转轴转动的最大角速度ω多大?
(3)若先剪断B处绳子,让转轴带动小球转动,使绳子与转轴的夹角从45°开始,直至小球能在最高位置作匀速圆周运动,则在这一过程中,小球机械能的变化为多大?
答案
解(1)B处绳被拉直时,绳与杆夹角θ=45°,TAcosθ=mg,
TAsinθ=m
,v2 L
∴v=gL
(2)此时,B绳拉力为TB=2mg,A绳拉力不变,TAcosθ=mg,
TAsinθ+TB=mω2L
∴ω=3g L
(3)小球在最高位置运动时,
=2mg,T ′A
cosα=mg,α=60°,T ′A
sinα=mT ′A
,得:vt=v 2t
Lsinα2 3
gL2 2
△E=mg
L(cosθ-cosα)+(2
m1 2
-v 2t
mv2)1 2
∴△E=
mgL(
+2)2 4
答:(1)当B处绳子刚好被拉直时,小球的线速度v=
.gL
(2)为不拉断细绳,转轴转动的最大角速度ω=
.3g L
(3)小球机械能的变化△E=
mgL.(
+2)2 4
