问题
问答题
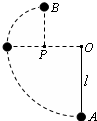
如图所示,质量为m的小球用长为l的轻质细线悬挂于O点,与O点处于同一水平线的P点处有一根光滑的细钉,已知OP=
,在A点给小球一个水平向左的初速度v0,发现小球恰好能到达跟P点在同一竖直线上的最高点B,则l 2
(1)小球到达B点时的速度是多大?
(2)若不计空气阻力,则给小球的初速度v0应该多大?
(3)若v0=2
,那么小球从点A到B的过程中克服空气阻力做功为多少?gl
答案
(1)因小球恰好能到达跟P点在同一竖直线上的最高点B,所以由圆周运动的知识得:
mg=m
①vB2 l 2
解得:vB=
②gl 2
(2)小球在从点A到B的过程中,只有重力对小球做功,故它的机械能是守恒的,以点A所在的平面为参考平面,由机械能守恒定律得
mv02=1 2
mvB2+mg•(l+1 2
)③l 2
解②、③两式,得v0=
④7gl 2
(3)因2
>gl
,小球恰好能到达跟P点在同一竖直线上的最高点B,所以在小球从点A到B的过程中要克服空气阻力做功,设此值为W,则由动能定理得-mg•(l+7gl 2
)-W=l 2
mvB2-1 2
mv02⑤1 2
解得 W=mgl 4
答:(1)小球到达B点时的速度是gl 2
(2)若不计空气阻力,则给小球的初速度应该是7gl 2
(3)小球从点A到B的过程中克服空气阻力做功为mgl 4
