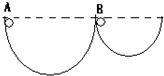
如图所示,两个半径不同而内壁光滑的半圆轨道固定在地面上,质量相等的两个小球分别从与球心在同一水平高度的A、B两点由静止开始自由滑下,它们通过轨道最低点时( )
A.速度相同
B.向心加速度相同
C.对轨道的压力相等
D.机械能相等
A、设半圆轨道的半径为r,小球到最低点的速度为v,由机械能守恒定律得:mgr=
mv2,所以v=1 2
由于它们的半径不同,所以线速度不等,故A错误;2gr
B、小球的向心加速度an=
,与上式联立可以解得:an=2g,与半径无关,因此此时小球的向心加速度相等,故B正确;v2 2g
C、在最低点,由牛顿第二定律得:FN-mg=m
,联立解得;FN=3mg,即压力为3mg,由于球的质量相等,所以对轨道的压力相同.故C正确.v2 r
D、A、B两点由静止开始自由下滑过程中,受到重力和支持力作用,但只有重力做功,机械能守恒,两球初位置的机械能相等,所以末位置的机械能也相等,故D正确.
故选BCD
