核聚变能以氘、氚等为燃料，具有安全、洁净、储量丰富三大优点，是最终解决人类能源危机的最有效手段．

（1）两个氘核

21

H结合成一个氦核

32

He时，要放出某种粒子，同时释放出能量，写出核反应的方程．若氘核的质量为m₁，氦核的质量为m₂，所放出粒子的质量为m₃，求这个核反应中释放出的能量为多少？

（2）要使两个氘核能够发生聚变反应，必须使它们以巨大的速度冲破库仑斥力而碰到一起，已知当两个氘核恰好能够彼此接触发生聚变时，它们的电势能为

e2

4πε0(2R)

（其中e为氘核的电量，R为氘核半径，ε₀为介电常数，均为已知），则两个相距较远（可认为电势能为零）的等速氘核，至少具有多大的速度才能在相向运动后碰在一起而发生聚变？

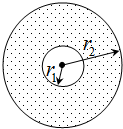
（3）当将氘核加热成几百万度的等离子状态时就可以使其获得所需速度．有一种用磁场来“约束”高温等离子体的装置叫做“托卡马克”，如图所示为其“约束”原理图：两个同心圆的半径分别为r₁和r₂，等离子体只在半径为r₁的圆形区域内反应，两圆之间的环形区内存在着垂直于截面的匀强磁场．为保证速率为v的氘核从反应区进入磁场后不能从磁场区域的外边界射出，所加磁场磁感应强度的最小值为多少？（不考虑速度大小对氘核质量的影响）