问题
问答题
如图所示,轻线一端系一质量为m的小球,另一端穿过光滑小孔套在正下方的图钉A上,此时小球在光滑的水平平台上做半径为a、角速度为ω的匀速圆周运动.现拔掉图钉A让小球飞出,此后细绳又被A正上方距A高为h的图钉B套住,达稳定后,小球又在平台上做匀速圆周运动.求:
(1)图钉A拔掉前,轻线对小球的拉力大小,
(2)从拔掉图钉A到被图钉B套住前小球做什么运动?所用的时间为多少?
(3)小球最后做圆周运动的角速度.

答案
(1)拔掉A图钉前,轻线的拉力为小球做圆周运动的向心力,设其大小为T,则由牛顿第二定律得:
T=mω2a
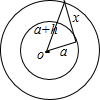
(2)拔掉A图钉小球沿切线方向匀速直线运动,直到线环B被图钉套住,小球的速度:v=ωa
小球的运动情况如图所示,则小球匀速运动的位移为:
x=
=(a+h)2-a2 2ah+h2
则运动时间:t=
=x v 2ah+h2 ωa
(3)v可分解为切向速度v1和法向速度v2,绳被拉紧后v2=0,小球以速度v1做匀速圆周运动,
半径:r=a+h
由于:v1=
v=a a+h
ωa2 a+h
解得:ω=
=v1 r a2ω (a+h)2
答:(1)图钉A拔掉前,轻线对小球的拉力大小为mω2a;
(2)从拔掉图钉A到被图钉B套住前小球沿切线方向做匀速直线运动,所用的时间为
;2ah+h2 ωa
(3)小球最后做圆周运动的角速度为
.a2ω (a+h)2
