问题
填空题
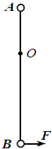
如图所示,A、B两小球质量均为m,被固定在一根长为L=1m的细长轻杆两端,可绕过O点的轴在竖直平面内无摩擦转动,OA=L/3.开始时,轻杆竖直,今在B球上施加一水平恒力F=
,g=10m/s2,则当杆转动的角度θ=______时,B球能获得最大速度,B球获得的最大速度vm=______m/s.
mg3 2
答案
当力矩平衡时,B球速度最大.
则F•
Lcosθ+mg•2 3
Lsinθ=mg1 3
Lsinθ2 3
解得θ=60°.
A、B的角速度大小相等,则A、B的线速度大小之比为1:2.
B球的速度为vm,A球的速度为vm 2
根据能量守恒定律得,F•
Lsinθ=mg•2 3
L(1-cosθ)+1 3
mvm2+1 2
m(1 2
)2vm 2
解得vm=
m/s.4 3 3
故答案为:60°、
.4 3 3
