问题
单项选择题
设x1、x2是关于x的方程x2-(m-1)x-m=0(m≠0)的两个根,且满足 ,则m的值为( )。
A.-1
B.1
C.2
D.3
答案
参考答案:D
解析:
因为△=[-(m-1)]2+4m=(m+1)2≥0,
所以对于任意实数m,方程恒有两个实数根x1,x2,
又因为x1+x2=m-1,x1x2=-m,且m≠0
故
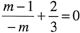 ,即m=3
,即m=3
故正确答案为D。
设x1、x2是关于x的方程x2-(m-1)x-m=0(m≠0)的两个根,且满足 ,则m的值为( )。
A.-1
B.1
C.2
D.3
参考答案:D
解析:
因为△=[-(m-1)]2+4m=(m+1)2≥0,
所以对于任意实数m,方程恒有两个实数根x1,x2,
又因为x1+x2=m-1,x1x2=-m,且m≠0
故
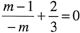 ,即m=3
,即m=3
故正确答案为D。