问题
问答题
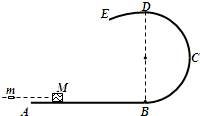
如图所示,ABCDE是由三部分光滑轨道平滑连接在一起组成的,AB为水平轨道,
是半径为R的半圆弧轨道,
BCD
是半径为2R的圆弧轨道,
DE
与
BCD
相切在轨道最高点D,R=0.6m.质量为M=0.99kg的小物块,静止在AB轨道上,一颗质量为m=0.01kg子弹水平射入物块但未穿出,物块与子弹一起运动,恰能贴着轨道内侧通过最高点从E点飞出.取重力加速度g=10m/s2,求: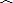
DE
(1)物块与子弹一起刚滑上圆弧轨道B点的速度;
(2)子弹击中物块前的速度;
(3)系统损失的机械能.
答案
(1)由物块与子弹一起恰能通过轨道最高点D,得:(M+m)g=(M+m)v 2D 2R
又由物块与子弹上滑过中根据机械能守恒得:
(M+m)1 2
+(M+m)g•2R=v 2D
(M+m)1 2 v 2B
代入数据解得:vB=
=6m/s6Rg
(2)由动量守恒 mv=(M+m)vB
v=600m/s
(3)根据能的转化和守恒定律得 △E=
mv2-1 2
(M+m)1 2 v 2B
代入数据得:△E=1782J
答:(1)物块与子弹一起刚滑上圆弧轨道B点的速度为6m/s.
(2)子弹击中物块前的速度为600m/s.
(3)系统损失的机械能为1782J.
