问题
问答题
如图所示,在直角坐标系的第II象限和第Ⅳ象限中的直角三角形区域内,分布着磁感应强度均为B=5.0×10-3T的匀强磁场,方向分别垂直纸面向外和向里.质量为m=6.64×10-27kg、电荷量为q=+3.2×10-19C的α粒子(不计α粒子重力),由静止开始经加速电压为U=1205V的电场(图中未画出)加速后,从坐标点M(-4,
)处平行于x轴向右运动,并先后通过两个匀强磁场区域.2
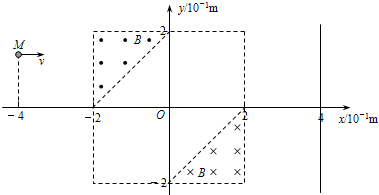
(1)请你求出α粒子在磁场中的运动半径;
(2)你在图中画出α粒子从直线x=-4到直线x=4之间的运动轨迹,并在图中标明轨迹与直线x=4交点的坐标;
(3)求出α粒子在两个磁场区域偏转所用的总时间.
答案
(1)粒子在电场中被加速过程,由动能定理得
:
qU=
mv2,得,v=1 2 2qU m
α粒子在磁场中偏转,由洛伦兹力提供向心力,则由牛顿第二定律得:
qvB=mv2 r
联立解得:
r=1 B
=2mU q 1 0.005
=2×6.64×10-27×1205 3.2×10-19
m2
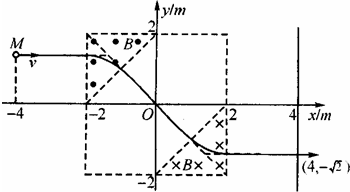
(2)由几何关系可得,α粒子恰好垂直穿过分界线,故正确图象如右图所示.
(3)带电粒子在磁场中的运动周期T=
=2πr v
=2.6×10-5s2πm qB
α粒子在两个磁场中分别偏转的弧度为
,在磁场中的运动总时间为t=π 4
T=1 4
=6.5×10-6sπm 2qB
答:
(1)α粒子在磁场中的运动半径为
m.2
(2)α粒子从直线x=-4到直线x=4之间的运动轨迹如图.
(3)α粒子在两个磁场区域偏转所用的总时间为6.5×10-6s.
