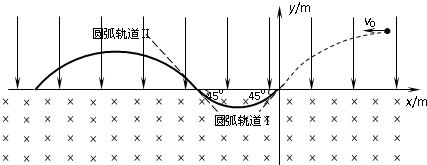
如图,在竖直面内的坐标系xoy中,x轴上方存在竖直向下的匀强电场,电场强度 E=12N/C,在x轴下方存在垂直纸面向里的匀强磁场,磁感应强度B=2T,一带电量为q=+3×10-4c、质量为m=3.6×10-4kg的小球,从(1m,0.5m)处以初速度v0沿x轴负方向抛出,刚好经坐标原点与x轴成45°,沿切线方向进入图中半径为R1=(2+)m的光滑圆弧轨道Ⅰ,再次经 x轴沿切线方向进入半径为R2=3(2+)m,的光滑圆弧轨道Ⅱ,求:(g取10m/s2)
(1)小球抛出时的初速度;
(2)小球到达轨道Ⅰ的最低点时对轨道的压力;
(3)若小球从从第一象限某位置沿x轴负向抛出后均能通过坐标原点沿切线方向进入轨道Ⅰ,再沿轨道Ⅱ外侧到达最高点,求小球抛出的所有可能位置.
(1)由题意知:Eq=mg=3.6×10-3N,则:a==2g=20m/s2
由y1=at2得 t=s
由x1=v0t 得 v0=2m/s
(2)设小球到达轨道Ⅰ最底点的速度为v1,所受支持力为FN,洛化兹力为FB,则:
m-m=(Eq+mg)y1+mgR1(1-cos45°)
代入数据得:v1=8m/s
在轨道Ⅰ的最低点,有 FN-FB-mg=m
代入数据得 FN=1.27×10-2N
即此时小球对轨道Ⅰ的压力为1.27×10-2N
(3)因小球达坐标原点时的速度偏向角为45°,则小球的位移偏向角正切值为0.5,即小球抛出点的位置必在方程y=x上.
(Ⅰ)设小球从(x2,y2)处以初速度v01抛出,达轨道Ⅱ最高点的速度为零,则:
0-m=(Eq+mg)[y2+R2(1-cos45°)]
代入数据并化简得:=40(3-y2)
由:y2=x2
a=v01t2得:20t2=v01
由上两式得:t2=s
v01=2(m/s)
故:x2=v01t=2×=3(m)
(Ⅱ)设小球从(x3,y3)处以初速度v02抛出,达轨道Ⅱ最高点的最大速度为v2,则:
m-m=(Eq+mg)[y3+R2(1-cos45°)]
Eq+mg=
代入数据并化简得:-60(2+)=40(3-y3)
得:t2=s
v02=m/s
则得 x02=t2v02=3(4-)m
由此可知:要让小球到达轨道Ⅱ的最高点,小球抛出的位置在y=x上,
区间为3m≤x≤3(4-)m
答:
(1)小球抛出时的初速度是2m;
(2)小球对轨道Ⅰ的压力为4.56×10-3N;
(3)要让小球到达轨道Ⅱ的最高点,小球抛出的位置在y=x上,区间为3m≤x≤3(4-)m.

