如图甲所示,在光滑绝缘的水平面上固定着两对几何形状完全相同的平行金属板PQ和MN,P、Q与M、N四块金属板相互平行地竖直地放置,其俯视图如图乙所示.已知P、Q之间以及M、N之间的距离都是d=0.2m,极板本身的厚度不计,极板长均为L=0.2m,板间电压都是U=6.0×102V.金属板右侧为竖直向下的匀强磁场,磁感应强度B=5×102T,磁场区域足够大.今有一质量为m=1×10-4kg,电量为q=2×10-6C的带负电小球在水平面上如图从PQ平行板间左侧中点O沿极板中轴线以初速度v0=4m/s进入平行金属板PQ.
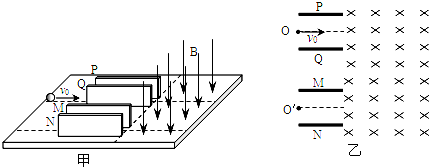
(1)试求小球刚穿出平行金属板PQ进入磁场瞬间的速度;
(2)若要小球穿出平行金属板PQ后,经磁场偏转射入平行金属板MN中,且在不与极板相碰的前提下,最终在极板MN的左侧中点O′沿中轴线射出.则金属板Q、M间距离最大是多少?
(1)小球在PQ金属板中做类平抛运动:
小球所受电场力F=qE=q
,U d
而小球加速度a=F m
故a=qU md
a=
m/s2=60m/s26×102×2×10-6 0.2×1×10-4
小球在板间运动的时间 t=
=L v0
s=0.05s 0.2 4
小球在垂直板方向上的速度 vy=at=60×0.05m/s=3m/s
则小球离开PQ板时的速度为vt=
=
+v 20 v 2y
m/s=5m/s 42+32
vt沿中轴线的夹角为tanθ=
=vy v0 3 4
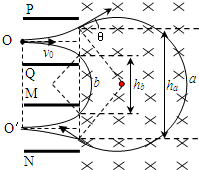
(2)在PQ极板间,若P板电势比Q板高,则小球向P板偏离,进入右侧磁场后做圆周运动,由运动的对称性,则必须N板电势高于M板电势,其运动轨迹如图a所示;同理若Q板电势比P板高,则必须M板电势高于N板电势,其运动轨迹如图b所示.否则不可能在不与极板相碰的前提下,最终在极板MN的左侧中点O′沿中轴线射出.
小球进入磁场后做圆周运动,设运动半径为R,因洛仑兹力提供向心力,即:
qvtB=mv 2t R
所以R=
=mvt Bq
m=0.5m 1×10-4×5 2×10-6×5×102
在PQ极板间,若小球向P板偏,设小球射入与射出磁场的两点间的距离为ha;在PQ极板间,若小球向Q板偏,设小球射入与射出磁场的两点间的距离为hb.由图中几何关系(注:图中半径不同,为简便,两图合一)可算得:
ha=hb=2Rcosθ=2×0.5×
m=0.8m 4 5
小球偏离中轴线的位移
Y侧=
at2=1 2
×60×0.052m=7.5×10-2m1 2
当小球向P板偏时,根据对称性可得QM板间的距离为 d1=ha-2(
+Y侧)=ha-d-2Y侧 d 2
当小球向Q板偏时,根据对称性可得QM板间的距离为d2=hb-2(
-Y侧)=hb-d+2Y侧 d 2
显然d2>d1
代入数据得 d2=hb-d+2Y侧=0.8-0.2+2×7.5×10-2m=0.75m
因而金属板Q、M间距离最大为0.75m.
答:(1)则小球刚穿出平行金属板PQ进入磁场瞬间的速度大小为5m/s,方向与轴线的夹角正切值为
;3 4
(2)若要小球穿出平行金属板PQ后,经磁场偏转射入平行金属板MN中,且在不与极板相碰的前提下,最终在极板MN的左侧中点O′沿中轴线射出.则金属板Q、M间距离最大是0.75m.
