问题
问答题
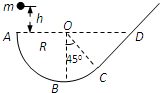
如图,竖直放置的斜面CD的下端与光滑圆弧轨道ABC的C端相切,圆弧半径为R,圆心与A、D在同一水平面上,∠COB=45°,现将一个质量为m的小物块从A点上方距A竖直高度为h=0.5R的位置无初速释放,小物块从A点进入轨道运动至斜面上D点后返回.
求:
(1)物块运动至A时的速度
(2)物块第一次运动至B时对轨道的压力
(3)物体与斜面CD之间的动摩擦因数.
答案
(1)设物块运动至A时的速度为vA,物块做自由落体运动vA =
=2gh gR
(2)物块第一次运动至B时速度为vB,从A运动到B的过程中机械能守恒,则:
mg(h+R)=
mvB21 2
设物块运动至B时轨道对物块的支持力为N,N-mg=mvB2 R
解得N=4mg
根据牛顿第三定律可知对轨道的压力为4mg
(3)由题意可知CD之间的距离为R,设物体与斜面CD之间的动摩擦因数为μ,
自开始下落至运动至D点,根据动能定理mgh-μmgRcos45°=0
解得μ=2 2
答:(1)物块运动至A时的速度为
;(2)物块第一次运动至B时对轨道的压力为4mg;(3)物体与斜面CD之间的动摩擦因数为gR
.2 2
