问题
问答题
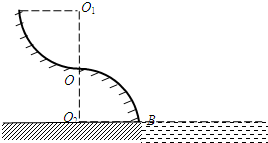
图中的AOB是游乐场中的滑道模型,它位于竖直平面内,由两个半径都是R的
圆周连接而成,它们的圆心O1、O2与两圆弧的连接点O在同一竖直线上.O2B沿水池的水面.一小滑块可由弧AO的任意点从静止开始下滑.1 4
(1)凡能在O点脱离滑道的小滑块,其落水点到O2的距离如何?
(2)若小滑块从开始下滑到脱离滑道过程中,在两个圆弧上滑过的弧长相等,则小滑块开始下滑时应在圆弧AO上的何处?(用该处到O1的连线与竖直线的夹角表示).
答案
(1)从A到O的运动过程中根据动能定理得:
mgR=
mv21 2
解得:v=2gR
设能脱离轨道的最小速度为v1
则有:mg=mv12 R
解得:v1=gR
R=
gt21 2
X=vot
联立得:
R≤x≤2R 2
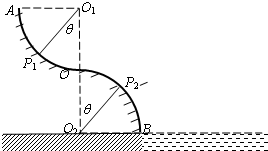
(2)如图所示,设滑块出发点为P1,离开点为P2,按题意要求O1P1、O2P2与竖直方向的夹角相等,
设其为θ,若离开滑道时的速度为v,则滑块在P2处脱离滑道的条件是m
=mgcosθv2 R
由机械能守恒 2mgR(1-cosθ)=
mv21 2
联立解得 cosθ=4 5
答:(1)凡能在O点脱离滑道的小滑块,其落水点到O2的距离范围为
R≤x≤2R; 2
(2)小滑块开始下滑时应在圆弧AO上的 cosθ=
处.4 5
