在水平地面上方的足够大的真空室内存在着匀强电场和匀强磁场共存的区域,且电场与磁场的方向始终平行,在距离水平地面的某一高度处,有一个带电量为q、质量为m的带负电的质点,以垂直于电场方向的水平初速度v0进入该真空室内,取重力加速度为g.求:
(1)若要使带电质点进入真空室后做半径为R的匀速圆周运动,求磁感应强度B0的大小及所有可能的方向;
(2)当磁感应强度的大小变为B时,为保证带电质点进入真空室后做匀速直线运动,求此时电场强度E的大小和方向应满足的条件;
(3)若带电质点在满足第(2)问条件下运动到空中某一位置M点时立即撤去磁场,此后运动到空中另一位置N点时的速度大小为v,求M、N两点间的竖直高度H及经过N点时重力做功的功率.
(1)由于带电质点在匀强电场E0和匀强磁场B0共存的区域做匀速圆周运动,
所以受到的电场力必定与重力平衡,
即 qE0=mg
根据牛顿第二定律和向心力公式
qv0B0=mv 20 R
解得 B0=mv0 qR
磁感应强度B0为竖直向上或竖直向下.
(2)磁场B和电场E方向相同时,如答图1甲所示;磁场B和电场E方向相反时,如答图1乙所示.
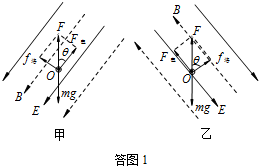
由于带电质点做匀速直线运动,由平衡条件和几何关系可知
(qv0B)2+(qE)2=(mg)2
解得 E=(mg)2-(qv0B)2 q
图中的θ角为 θ=arcsinqv0B mg
即电场E的方向为沿与重力方向夹角θ=arcsin
且斜向下的一切方向,qv0B mg
或θ=arctan
=qv0B qE
,且斜向下方的一切方向. qv0B (mg)2-(qv0B)2
(3)当撤去磁场后,带电质点只受电场力和重力作用,这两个力的合力大小为qv0B,方向既垂直初速度v0的方向也垂直电场E的方向.
设空中M、N两点间的竖直高度为H,因电场力在这个过程中不做功,则由机械能守恒定律得
m v2=mgH+1 2
m v02 1 2
解得 H=v2- v 20 2g
因带电质点做类平抛运动,由速度的分解可求得带电质点到达N点时沿合力方向的分速度大小为
vN=v2- v 20
又因电场力在这个过程中不做功,带电质点到达N点时,重力做功的功率等于合外力在此时的瞬时功率,
解得 PN=qv0BvN=qv0Bv2- v 20
答:(1)若要使带电质点进入真空室后做半径为R的匀速圆周运动,则磁感应强度B0的大小
及所有可能的方向为竖直向上或竖直向下;mv0 qR
(2)当磁感应强度的大小变为B时,为保证带电质点进入真空室后做匀速直线运动,则此时电场强度E的大小 E=
方向应满足的条件为电场E的方向为沿与重力方向夹角θ=arcsin(mg)2-(qv0B)2 q
且斜向下的一切方向,或θ=arctanqv0B mg
=qv0B qE
,且斜向下方的一切方向. qv0B (mg)2-(qv0B)2
(3)若带电质点在满足第(2)问条件下运动到空中某一位置M点时立即撤去磁场,此后运动到空中另一位置N点时的速度大小为v,则M、N两点间的竖直高度H及经过N点时重力做功的功率为=qv0B
.v2- v 20
