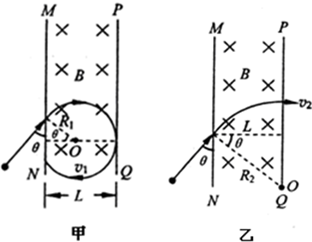
如图所示,在真空区域内,有宽度为L的匀强磁场,磁感应强度为B,磁场方向垂直纸面向里,MN、PQ是磁场的边界.质量为m,带电量为-q的粒子,先后两次沿着与MN夹角为θ(0<θ<90°)的方向垂直磁感线射入匀强磁场B中,第一次,粒子是经电压U1加速后射入磁场,粒子刚好没能从PQ边界射出磁场.第二次粒子是经电压U2加速后射入磁场,粒子则刚好垂直PQ射出磁场.不计重力的影响,粒子加速前速度认为是零,求:加速电压
的值.U1 U2

经电压U1加速后粒子射入磁场后刚好不能从PQ边界射出磁场,表明在磁场中做匀速圆周运动的轨迹与PQ边界相切,要确定粒子做匀速圆周运动的圆心O的位置,如图甲所示,圆半径R1与L的关系式为:L=R1+R1cosθ,R1=L 1+cosθ
又 qv1B=m v 21 R
解得v1=BqL m(1+cosθ)
经电压U2加速后以速度v2射入磁场,粒子刚好垂直PQ射出磁场,可确定粒子在磁场中做匀速圆周运动的圆心在PQ边界线的O点,如图乙所示,半径R2与磁场宽L的关系式为 R2=L cosθ
又qv2B=m v 22 R
解得v2=BqL mcosθ
在加速电场中,根据动能定理得 U1q=
m1 2
U2q=v 21
m1 2 v 22
所以
=U1 U2
=v 21 v 22 cos2θ (1+cosθ)2
答:加速电压
的值等于U1 U2
.cos2θ (1+cosθ)2