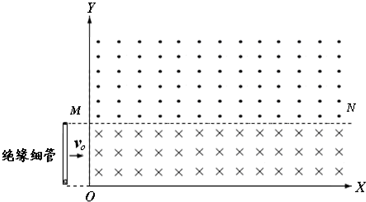
如图所示,在X>0,Y>0的空间中存在两个以水平面MN为界,磁感应强度大小均为B,方向相反的匀强磁场.一根上端开口、内壁光滑的绝缘细管,长为L,其底部有一质量为m、电量为+q的粒子.在水平外力作用下,保持细管始终平行于Y轴,沿X方向以速度v0匀速向右运动,且B=
,不计粒子的重力.求:mv0 2qL
(1)细管刚进入磁场时,粒子运动的加速度大小、方向;
(2)维持细管始终平行于Y轴向右匀速运动的过程中,水平外力所做的功;
(3)粒子第一次到达运动轨迹最高点的位置坐标.
(1)以粒子为研究对象,粒子刚进入磁场f1=qv0B a1=
=qv0B m
沿+Y方向 v02 2L
(2)粒子离开玻璃管前,在管中竖直方向做匀加速直线运动,水平方向做匀速运动,设粒子在管中竖直方向做加速运动的加速度a,粒子运动到管口时,粒子在竖直方向的分速为v1,则
在竖直方向 a=a1 v12=2aL
可解得 v1=v0
粒子离开玻璃管口时的速度 v′=
=v2+ v 21
v0m/s2
速度方向与MN成45°角
外力所做的功,
有功能关系 WF=△Ek △EK=
m1 2 v 20
可得 WF=
m1 2 v 20
(3)粒子离开管口后,在磁场中做匀速圆周运动
在磁场中 qv′B=m
r=v′2 r
=2mv′ qB
L2
粒子在管中运动的时间t =
=L v1 2 2L v0
粒子在管中运动的过程中发生的水平位移△x=v0t=2L
轨迹最高点的位置坐标:x=△x+r•sin45°=4L y=L+r(1-cos450)=(2
-1)L..2
