问题
问答题
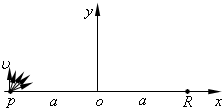
如图所示．一簇质量均为m、电量均为q的离子，在P点以同一速率v沿xoy上半平面中的各个方向射出，在P点左侧靠近P点处有一竖直放置的挡板．现加一垂直于xoy平面的磁感应强度为B的有界匀强磁场，可将这些离子聚焦到R点，P点与R点相距为2a，离子轨迹关于y轴对称．试求：
（1）离子在磁场中运动的轨迹半径
（2）当
=a时，与x轴成30°角射出的离子从P点到达R点的时间．mv Bq
（3）试推出在x＞0的区域中磁场的边界点坐标x和y满足的关系式．（没有问题，最多改为“x、y满足的关系式”）
答案
（1）离子进入磁场后，受洛仑兹力作用，由牛顿第二定律得：
Bqv=mv2 r
整理得：r=mv qB
（2）如图所示，由几何关系可得，离子进入磁场A点坐标为（-
，a 2
a）离开磁场B点坐标为（3 6
，a 2
a）3 6
由几何关系，离子运动的路程为：
s=
a+2 3 3
r=π 3
a+2 3 3
aπ 3
则t=
=s v
或t=(2
+π)a3 3v
=s v (2
+π)m3 3Bq
（3）在x＞0的区域内，令离子离开磁场后与x轴夹角为θ．
由几何关系得：x=rsinθ
y=(
-rtanθ)sinθa cosθ
代入相关数据并化简得：y=(ax-x2)Bq m2v2-B2q2x2
答：（1）离子在磁场中运动的轨迹半径r=mv qB
（2）当
=a时，与x轴成30°角射出的离子从P点到达R点的时间t=mv Bq
或t=(2
+π)a3 3v
．(2
+π)m3 3Bq
（3）在x＞0的区域中磁场的边界点坐标x和y满足关系式y=
．(ax-x2)Bq m2v2-B2q2x2