如图所示,平面直角坐标系xoy中,在第二象限内有竖直放置的两平行金属板,其中右板开有小孔;在第一象限内存在内、外半径分别为
R、R的半圆形区域,其圆心与小孔的连线与x轴平行,该区域内有磁感应强度为B的匀强磁场,磁场的方向垂直纸面向里:在y<0区域内有电场强度为E的匀强电场,方向与x轴负方向的夹角为60°.一个质量为m,带电量为-q的粒子(不计重力),从左金属板由静止开始经过加速后,进入第一象限的匀强磁场.求3 3
(1)若两金属板间的电压为U,粒子离开金属板进入磁场时的速度是多少:
(2)若粒子在磁场中运动时,刚好不能进入
R的中心区域,此情形下粒子在磁场中运动的速度大小.3 3
(3)在(2)情形下,粒子运动到y<0的区域,它第一次在匀强电场中运动的时间.

(1)设当加速电压为U时,粒子离开金属板时的速度为v1,
则有:qU=
m1 2 v 21
解得:v1=2qU m
(2)此情形下粒子在磁场中运动的轨迹如图所示,设粒子运动速度为v2,运动圆半径为r,
由几何知识得:r2+R2=(r+
R)23 3
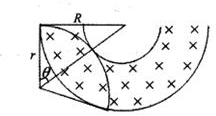
tanθ=R r
解得:r=
R,θ=60° 3 3
粒子在磁场中运动时,有:Bqv2=mv 22 r
解得:v2=
BqR3 3m
(3)粒子进入y<0的区域,做减速运动,设速度减少到零所用时间为t,
则:qE=ma
v2-at=0
解得:t=
BR3 3E
粒子第一次在匀强电场中的运动时间
T=2t=2
BR3 3E
答:(1)若两金属板间的电压为U,粒子离开金属板进入磁场时的速度是
;2qU m
(2)若粒子在磁场中运动时,刚好不能进入
R的中心区域,此情形下粒子在磁场中运动的速度大小为3 3
.
BRq3 3m
(3)在(2)情形下,粒子运动到y<0的区域,它第一次在匀强电场中运动的时间
.2
BR3 3E
