问题
问答题
如图,一匀强磁场磁感应强度为B,方向垂直纸面向里,其边界是半径为R的圆.MN为圆的一直径.在M点有一粒子源可以在圆平面内向不同方向发射质量m、电量-q速度为v的 粒子,粒子重力不计,其运动轨迹半径大于R.
(1)求粒子在圆形磁场中运动的最长时间(答案中可包含某角度,需注明该角度的正弦或余弦 值);
(2)试证明:若粒子沿半径方向入射,则粒子一定沿半径方向射出磁场.

答案
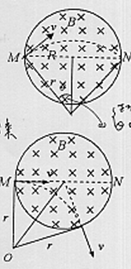
(1)若要粒子在磁场中运动的时间最长,则对应的圆心角最大.所以当运动轨迹的弦长等于磁场的直径时,满足题意.
由洛伦兹力提供向心力:Bqv=mv2 r
得:r=mv qB
图中:sinθ=
=R r BqR mv
运动的最长时间:
t=
=2θ•r v
(公式中sinθ=2mθ qB
)Bqv mv
(2)证明:如图所示,当粒子沿半径的方向射入时,r与R垂直,而出射速度v的方向与轨迹的半径r垂直,
所以出射速度与R在同一条直线上,即粒子一定沿半径方向射出磁场.证毕.
答:(1)子在圆形磁场中运动的最长时间
(公式中sinθ=2mθ qB
).(2)证明略.Bqv mv
