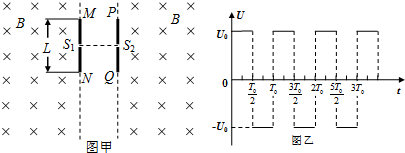
如图所示,相隔一定距离的竖直边界两侧为相同的匀强磁场区,磁场方向垂直纸面向里,在边界上固定两长为L的平行金属极板MN和PQ,两极板中心各有一小孔S1、S2,两极板间电压的变化规律如图乙所示,正反向电压的大小均为U0,周期为T0.在t=0时刻将一个质量为m电量为-q(q>0)的粒子由S1静止释放,粒子在电场力的作用下向右运动,在t=
时刻通过S2垂直于边界进入右侧磁场区.(不计粒子重力,不考虑极板外的电场)T0 2
(1)求粒子到达S2时的速度大小v和极板间距d;
(2)为使粒子不与极板相撞,求磁感应强度的大小应满足的条件.
(3)若已保证了粒子未与极板相撞,为使粒子在t=3T0时刻再次到达S2,且速度恰好为零,求该过程中粒子在磁场内运动的时间和磁感应强度的大小.
(1)粒子在匀强电场中电场力做功等于粒子动能的增加,得:
qU0=
mv21 2
代入数据,得:v=2qU m
又:d=
v(1 2
),T0 2
联立以上两式,得:d=T0 4 2qU0 m
(2)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,即:qvB=
,mv2 r
得:r=mv qB
使粒子不与极板相撞,则运动的半径r≥L 4
联立以上两式,得:B≤4 L 2mU0 q
(3)粒子在t=3T0时刻再次到达S2,且速度恰好为零,则从s1再次进入电场时的时刻是
;粒子在左右磁场中的时间是相等的,故从右向左穿过电场的中间时刻是5T0 2
,通过与图乙比较,可以知道从右向左穿过电场时,前半段做减速运动,后半段做加速运动,前后对称.设粒子减速运动时间t时,位移恰好是3T0 2
,粒子受到的电场力:F=qEd 2
电场强度:E=
,U d
加速度:a=-
,F m
粒子做减速运动,
=vt+d 2
at21 2
联立以上几个公式,解得:t=
(T0 2
)2- 2 2
粒子在磁场中运动的总时间:t′=
-5T0 2
-2×t=T0 2
T02+ 2 2
粒子在左右磁场中的时间是相等的且都是半个周期,所以粒子运动的总时间是一个周期,即t′=T;粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,得:
qvB=
,vT=2πrm4π2r T2
得:B=
.4πm (2+
)qT02
答:(1)粒子到达S2时的速度
和极板间距d=2qU m T0 4
;2qU0 m
(2)磁感应强度的大小应满足的条件B≤4 L
;2mU0 q
(3)粒子在磁场内运动的时间t′=
T0,磁感应强度的B=2+ 2 2
.4πm (2+
)qT02
