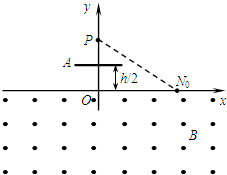
如图,在x轴下方有匀强磁场,磁感应强度大小为B,方向垂直于x y平面向外.P是y轴上距原点为h的一点,N0为x轴上距原点为a的一点.A是一块平行于x轴的挡板,与x轴的距离为
,A的中点在y轴上,长度略小于h 2
.带电粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变.质量为m,电荷量为q(q>0)的粒子从P点瞄准N0点入射,最后又通过P点.不计重力.a 2
(1)若粒子从P点射出的速率为v,求粒子在磁场中运动的轨道半径R;
(2)求粒子从N0点射入磁场到第一次穿出磁场所经历的时间.(可用反三角函数表示)
(3)求粒子入射速度的所有可能值.
(1)当粒子的入射速度为v时,粒子在磁场中运动的轨道半径为R,
由qvB=m
①v2 R
得轨道半径R=
②mv qB
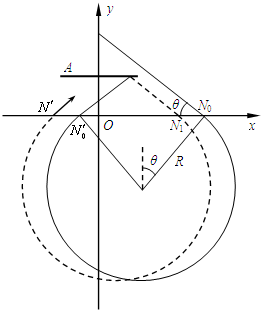
(2)如图所示,第一次射出磁场的点为N′,粒子与A板碰撞后再次进入磁场的位置为N1.
sinθ=
=PO PN0
③h a2+h2
粒子作匀速圆圆运动的周期为T=
=2πR v
④2πm qB
则粒子从N0点射入磁场到第一次穿出磁场所经历的时间为
t=
T=2π-2θ 2π
•π-θ π 2πm qB
=
(π-arcsin2m qB
)⑤h a2+h2
(3)粒子与A板碰撞后再次进入磁场的位置为N1.粒子速率不变,每次进入磁场与射出磁场位置间距离x1保持不变,有
x1=N0′N0=2Rsinθ⑥
粒子射出磁场与下一次进入磁场位置间的距离x2始终不变,与N0′N1相等.
由图可以看出:x2=a⑦
设粒子最终离开磁场时,与档板相碰n次(n=0、1、2、3…).若粒子能回到P点,由对称性,
出射点的x坐标应为-a,
即(n+1)x1-nx2=2a ⑧
由⑦⑧两式得x1=
a ⑨n+2 n+1
若粒子与挡板发生碰撞,有x1-x2>
⑩a 4
联立⑦⑨⑩得 n<3
联立②⑥⑨得v=
•qB 2msinθ
an+2 n+1
把sinθ=
代入上式中得h a2+h2
当n=0,v0=qBa a2+h2 mh
当n=1,v1=3qBa a2+h2 4mh
当n=2,v2=2qBa a2+h2 3mh
答:(1)粒子在磁场中运动的轨道半径R=
.mv qB
(2)粒子从N0点射入磁场到第一次穿出磁场所经历的时间为
(π-arcsin2m qB
).h a2+h2
(3)粒子入射速度的可能值为
,qBa a2+h2 mh
,3qBa a2+h2 4mh
.2qBa a2+h2 3mh
