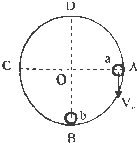
如图是半径为R=0.5m的光滑圆弧形轨道,直径AC水平,直径CD竖直.今有质量为m=1kg的小球a从A处以初速度v0=3
m/s沿圆弧运动,与静止在圆弧底端B处直径相同的小球b发生碰撞.则(g=10m/s2)6
(1)小球a在A处对轨道的压力多大?(结果保留两位有效数字)
(2)若小球b质量也为m,且a、b发生弹性碰撞,则碰后小球b的速度多大?
(3)若小球b质量为km(k>0),且a、b碰后粘在一起,欲使ab不脱离轨道求k的取值范围.
(1)设小球a在A点受到的支持力为FN,则
FN=mv 20 R
代入数据解得FN=108N
由牛顿第三定律可知小球a对轨道的压力等于FN即108N.
(2)小球a由A到B过程中机械能守恒,设小球a到达B点的速度为v,则
mgR=
mv2-1 2
m1 2 v 20
代入数据可解得 v=8m/s
碰撞过程a、b组成的系统动量守恒、机械能守恒,设碰后a、b球速度分别为va、vb 则
mv=mva+mvb
mv2=1 2
m1 2
+v 2a
m1 2 v 2b
由以上三式可解得 va=0,vb=v; va=v,vb=0(不合舍去)
故碰后b球速度为vb=8m/s
(3)设碰后ab的速度为vab,到达D点的速度为V,则
mv=(km+m)V
(km+m)1 2
≤(km+m)gR v 2ab
或
(km+m)1 2
=v 2ab
(km+m)V2+(km+m)•2R ③1 2
(km+m)
≥(km+m)g ④V2 R
由①②解得k≥
-132 5
由①③④解得k≤0.6
故欲使ab不脱离轨道须k≥
-1或k≤0.632 5
答:(1)小球a在A处对轨道的压力是108N.
(2)若小球b质量也为m,且a、b发生弹性碰撞,则碰后小球b的速度是8m/s.
(3)若小球b质量为km(k>0),且a、b碰后粘在一起,欲使ab不脱离轨道求k的取值范围是k≥
-1或k≤0.6.32 5
