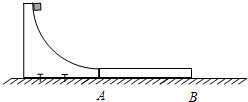
如图所示,一质量M=2.0kg的长木板AB静止在水平面上,木板的左侧固定一半径R=0.60m的四分之一圆弧形轨道,轨道末端的切线水平,轨道与木板靠在一起,且末端高度与木板高度相同.现在将质量m=1.0kg的小铁块(可视为质点)从弧形轨道顶端由静止释放,小铁块到达轨道底端时的速度v0=3.0m/s,最终小铁块和长木板达到共同速度.忽略长木板与地面间的摩擦.取重力加速度g=10m/s2.求
(1)小铁块在弧形轨道末端时所受支持力的大小F;
(2)小铁块在弧形轨道上下滑过程中克服摩擦力所做的功Wf;
(3)小铁块和长木板达到的共同速度v.
(1)小木块在弧形轨道末端时,由牛顿第二定律得
F-mg=m v 20 R
解得:F=mg+m
=1×10+1×v 20 R
=25N32 0.6
(2)铁块在弧形轨道上滑行过程,根据动能定理得
mgR-Wf=
m1 2
-0v 20
解得:克服摩擦力所做的功Wf=mgR-
m1 2
=1×10×0.6-v 20
×1×32=1.5J1 2
(3)铁块在木板上滑动过程,系统的动量守恒,则有 mv0=(m+M)v
解得:共同速度v=
=mv0 m+M
=1.0m/s1×3 1+2
答:
(1)小铁块在弧形轨道末端时所受支持力的大小F是25N;
(2)小铁块在弧形轨道上下滑过程中克服摩擦力所做的功Wf是1.5J.
(3)小铁块和长木板达到的共同速度v是1m/s.
