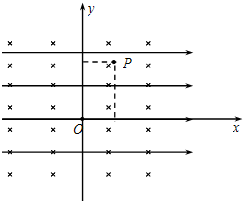
如图所示,匀强磁场方向垂直纸面向里,匀强电场方向水平向右,直角坐标系x0y的原点O处有一能向各个方向发射带电粒子(不计重力)的放射源、当带电粒子以某一初速度沿y轴正方向射入该区域时,恰好能沿y轴做匀速直线运动.若撤去磁场只保留电场,粒子以相同的速度从O点射入,经过一段时间后通过第一象限的P点,P点坐标为(L,
L).若撤去电场,只保留磁场,让粒子以相同速率从O点射入,求:3
(1)粒子在磁场中运动的半径;
(2)若要使粒子射出后仍能通过P点,求粒子从O点射出时的速度方向.
(1)电磁场同时存在时,由粒子做匀速直线运动,设入射速度大小为v0得:
qv0B=qE…①
撤去磁场后,粒子在电场中做曲线运动,将合运动沿着x、y方向正交分解,根据分位移公式,有
L=v0t…②3
L=
×1 2
×t2…③qE m
只保留磁场时,粒子在磁场中做圆周运动:
qv0B=m
…④v 20 R
联立以上各式解得:R=
L…⑤3 2
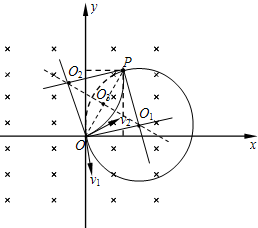
(2)连接OP,作OP的中垂线交OP于O3点,若粒子沿v1方向射出,圆心为O1,据已知条件有:
=. OO1
=R=. O1P
L…⑥3 2
=2L. OP
=. OO3
=L…⑦. O3P
据几何关系有:cos∠O3OO1=
=. O3O . OO1
…⑧2 3
因v1与
垂直,因此v1与x轴正方向所成夹角为∠O3OO1+30°,即arccos. OO1
+30°…⑨2 3
若粒子沿v2方向射出,同理可解得:cos∠O3OO2=
=. O3O . OO2 2 3
因v2与
垂直,因此v2与x轴 正方向 所 成 夹 角 为∠O3OO2-30°,即arccos. OO2
-30°…⑩2 3
答:(1)粒子在磁场中运动的半径为
L;3 2
(2)若要使粒子射出后仍能通过P点,粒子从O点射出时的速度方向与x轴成arccos
+30°角度斜向上或与x轴成arccos2 3
-30°角度斜向下.2 3
