问题
问答题
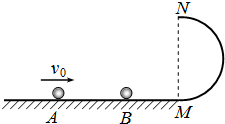
在光滑的水平面上,一质量为mA=0.1kg的小球A,以8m/s的初速度向右运动,与质量为mB=0.2kg的静止小球B发生弹性正碰.碰后小球B滑向与水平面相切、半径为R=0.5m的竖直放置的光滑半圆形轨道,且恰好能通过最高点N后水平抛出.g=10m/s2.求:(1)碰撞后小球B的速度大小;
(2)小球B从轨道最低点M运动到最高点N的过程中所受合外力的冲量;
(3)碰撞过程中系统的机械能损失.
答案
(1)小球B在最高点N时,由牛顿第二定律得:
mBg=mB
,解得:vN=v 2N R
m/s;5
小球从最低点运动到最高点的过程中,
由动能定理得:-2mBgR=
mBvN2-1 2
mBvM2,1 2
解得:vM=5m/s;
(2)以向右为正方向,从M到N过程,
由动量定理得:I=mBvN-mBvM=-(
+1)N•s,方向向左;5 5
(3)碰撞过程动量守恒,由动量守恒定律得:
mAv0=mAvA+mBvB,vB=vM,解得:vA=-2m/s;
碰撞过程中,由能量守恒定律可得:
损失的机械能为△E=
mAv02-1 2
mAvA2-1 2
mBvB2=0.5J;1 2
答:(1)碰撞后小球B的速度大小为5m/s;
(2)小球B从轨道最低点M运动到最高点N的过程中所受合外力的冲量大小为(
+1)N•s,方向向左;5 5
(3)碰撞过程中系统的机械能损失为0.5J.
