问题
多选题
如图所示,两个半径相同的半圆形光滑轨道置于竖直平面内,左右两端点等高,分别处于沿水平方向的匀强电场和匀强磁场中.两个相同的带正电小球同时从两轨道左端最高点由静止释放.M、N为轨道的最低点,则下列说法中正确的是( )
A.两个小球到达轨道最低点的速度vM<vN
B.两个小球第一次经过轨道最低点时对轨道的压力FM>FN
C.小球第一次到达M点的时间大于小球第一次到达N点的时间
D.在磁场中小球能到达轨道的另一端最高处,在电场中小球不能到达轨道另一端最高处
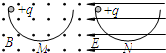
答案
A、对左图,根据动能定理得,mgR=
mvM2,解得vM=1 2
.2gR
对右图,根据动能定理得,mgR-qER=
mvN2,解得vN=1 2
.所以vM>vN.故A错误.2(mgR-qER) m
B、在最低点,对左图有:FM-mg=m
,解得FM=3mg.vM2 R
对右图有:FN-mg=m
,解得FN=3mg-qE.知FM>FN.故B正确.vN2 R
C、左图在运动的过程中,只有重力做功,右图在运动的过程中,除重力做功外,还有电场力做负功,起阻碍作用,所以小球第一次到达M点的时间小于小球第一次到达N点的时间.故C错误.
D、若在磁场中小球能运动到另一端的最高处,则根据动能定理知,在电场中,电场力始终做负功,小球不能到达最高点.故D正确.
故选BD.
