问题
问答题
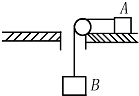
如图所示,水平转盘的中心有一竖直的小圆筒,质量为m的物体A放在转盘上,A到竖直筒中心的距离为r,物体A通过轻绳跨过无摩擦的滑轮与物体B相连,B与A的质量相同,物体A与转盘间的最大静摩擦力是正压力的μ(μ<1)倍,重力加速度为g,则转盘转动的角速度ω在什么范围内,物体A才能随转盘转动?
答案
取物体A为研究对象,物体A随转盘转动的向心力应由绳的拉力和摩擦力提供,摩擦力可能为零,可能指向圆心,也可能背离圆心,
绳的拉力F总等于B物体的重力mg.
若A物体随转盘转动的角速度较大,则A要沿转盘外滑,此时绳的拉力与最大静摩擦力的合力提供向心力,由牛顿第二定律得:mg+μmg=mrω12
解得ω1=
.g(1+μ) r
若A物体随转盘转动的角速度较小,则A要向圆心滑动,此时静摩擦力的方向背离圆心,由牛顿第二定律得:mg-μmg=mrω22
解得ω2=g(1-μ) r
要使A随转盘一起转动,则角速度ω应满足的关系是:
≤ω≤g(1-μ) r
.g(1+μ) r
答:转盘转动的角速度ω在
≤ω≤g(1-μ) r
范围内,物体A能随转盘转动.g(1+μ) r
