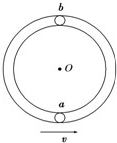
如图所示光滑管形圆轨道半径为R(管径远小 于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
A.当小球b在最高点对轨道无压力时,小球a比小球b所需向心力大5mg
B.当v=时,小球b在轨道最高点对轨道有压力
C.速度v至少为,才能使两球在管内做圆周运动
D.只要v≥ | 5gR,小球a对轨道最低点的压力比小球b对轨道最高点的压力大6mg |
A、b在最高点无压力时,向心力F1=mg;a在最低点时,向心力F2=m=5mg;即a球比b球所需向心力大4mg;故A错误;
B、当小球对轨道无压力时,则有:mg=m,解得:v1=;即当速度为时,小球在轨道最高点对轨道无压力;
由机械能守恒定律可得,mg2R=mv22-mv12;
求出小球在最低点时的速度v2=,当速度为时,小球在最高点对轨道无压力;故B正确;
C、因小球在管内转动,则内管可对小球提供向上的支持力,故可看作是杆模型;
故小球的最高点的速度只要大于等于零,小球即可通过最高点,结合B项分析可知C错误;
D、在最高点时,T1+mg=m
最低点时,T2-mg=m
T2-T1=2mg+m(-)
由机械能守恒定律可得,mg2R=mv22-mv12;
要使小球a对轨道最低点的压力比小球b对轨道最高点的压力大6mg,则要m(-)=4mg,由A分析可知当b在最高点无压力时,m(-)=4mg,再根据B项分析可知,当速度为时,小球在最高点对轨道无压力,则当v≥,小球a对轨道最低点的压力比小球b对轨道最高点的压力大6mg,故D正确.
故选BD