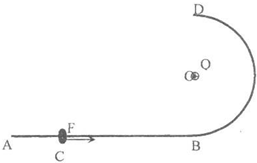
一端弯曲的光滑绝缘杆ABD固定在竖直平面上,如图所示,AB段水平,BD段是半径为R的半圆弧,有电荷量为Q(Q>0)的点电荷固定在圆心O点.一质量为m、电荷量为q(q>0)的带电小环套在光滑绝缘杆上,在水平外力作用下从C点由静此开始运动,到B点时撤去外力,小环继续运动,发现刚好能到绝缘杆的最高点D.已知CB间距为4R/3.(提示:根据电磁学有关知识,在某一空间放一电荷量为Q的点电荷,则距离点电荷为r的某点的电势为ϕ=k,其中k为静电力常量,设无穷远处电势为零.)
(1)求小环从C运动到B过程中,水平外力做的功;
(2)若水平外力为恒力,要使小环能运动到D点,求水平外力的最小值F0;
(3)若水平外力为恒力,大小为F(F大于(2)问中的F0),求小环运动到D点时,绝缘杆对环的弹力大小和方向.
(1)小球从C运动到B,带电小环要克服电场力做功,克服电场做的功W电等于电势能的增加,
则 W电=q-,
所以W电=,
小球从C运动到B,设到B得速度为VB,水平外力做的功为W,
则 W-W电=m
小球从B到D过程中,带电小环在等势面上运动电场力不做功,设到D点的速度为VD
则-2mgR=m-m
又刚好到D点,则D点速度为VD=0,
所以W=2mgR+,
(2)小球要能运动到D点,则VD≥0
由C运动到D点,F′•R-W电-2mgR=m
由此可以解得F′≥mg+
所以水平外力的最小值为F0=mg+.
(3)由C运动到D点,设D点速度为VD,
F•R-2mgR-=m
小环运动到D点时,设绝缘杆对小环的弹力大小为FN,方向指向圆心,
=FN+mg-
由此可得FN=F+-5mg
讨论:
(a)若F+>5mg,则弹力大小为F+-5mg,方向指向圆心.
(b)若F+=5mg,则弹力为零.
(c)若F+<5mg,则弹力大小为5mg-(F+),方向背向圆心.