问题
问答题
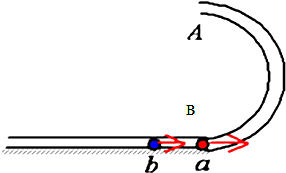
如图所示,半径为R内径很小的光滑半圆管竖直放置,和水平面相切与B处,两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点A时对管壁恰好没有作用力,b通过最高点A时,对管壁下部的压力为0.75mg,求:
(1)a、b两球落地点间的距离
(2)a球在刚好进入管道B处时对管壁的压力大小.
答案
(1)以a球为对象,设其到达最高点时的速度为va,根据向心力公式有:
mg=mva2 R
所以:va=
.gR
以b球为对象,设其到达最高点时的速度为vb,根据向心力公式有:
mg-Fb=m
.vb2 R
即
mg=m1 4
所以:vb=vb2 R 1 2 gR
a、b两球脱离轨道的最高点后均做一平抛运动,所以a、b两球的水平位移分别为:
xa=
×gR
=2R4R g
xb=vbt=1 2
×gR
=R4R g
故a、b两球落地点间的距离△x=xa-xb=R.
(2)对a球从B到A的过程中有
mg•2R=
mv2-1 2
mva21 2
F-mg=mv2 R
F=6mg.
答:(1)a、b两球落地点间的距离为R.
(2)a球在刚好进入管道B处时对管壁的压力大小为6mg.
