一条长为L的细线，上端固定，下端拴一质量为m的带电小球，将它置

问题问答题

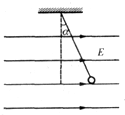
一条长为L的细线，上端固定，下端拴一质量为m的带电小球，将它置于一匀强电场中，电场强度大小为E，方向水平向右．已知当细线离开竖直位置的偏角为α为30°时，小球处于平衡，如图所示．问：

（1）小球带何种电荷？

（2）小球所带的电量是多少？

（3）如果细线的偏角由α向右增大到90°，然后将小球由静止开始释放，则小球运动到悬点正下方位置时，绳上拉力多大？

答案

（1）由图可知，小球所受电场力方向水平向右，场强也水平向右，则小球带正电荷．

（2）以小球为研究对象，分析受力，作出力图如图．根据平衡条件得

qE=mgtanα

得到q=

（3）将细线的偏角由α向右增大到90°，由静止开始释放后，设小球运动到到悬点正下方位置时速度为v，根据动能定理得

mgL-qEL=

mv2

又qE=mgtanα

得到mgL-mgLtanα=

mv2①

又由牛顿第二定律得，T-mg=m

②

联立①②解得

T=（3-

）mg

答：

（1）小球带正电荷．

（2）小球所带的电量是

．

（3）如果细线的偏角由α向右增大到90°，然后将小球由静止开始释放，小球运动到悬点正下方位置时，绳上拉力是（3-

）mg．