问题
问答题
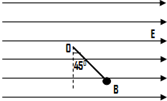
如图所示,一条长为L的细线上端固定在O点,下端系一个质量为m的小球,将它置于一个很大的方向水平向右的匀强电场中,已知小球在B点时平衡,细线与竖直线的夹角为45°,求:
(1)现将小球提至某一位置悬线伸直,试通过计算说明此时悬线与竖直方向夹角应为多大,才能使小球由静止释放后运动至最低点时,小球速度恰好为零?
(2)当细线与竖直方向成45°角时,至少要给小球一个多大的速度,才能使小球做完整的圆周运动?(结果可保留根号)
答案
(1)小球静止在B点时,根据平衡条件得
mgsin45°=Fcos45°
得到,电场力F=mg
从释放点到最低点过程,根据动能定理得
mgL(1-cosα)-FLsinα=0
得到,sinα+cosα=1
解得,α=90°
(2)设当小球运动到关于B对称的A点时,临界速度为vA.根据牛顿第二定律得
Fsin45°+mgsin45°=mv 2A L
解得,vA=2gL
由A到B过程,根据动能定理得
mg2Lcos45°+F2Lsin45°=
m1 2
-v 2B
m1 2 v 2A
解得,vB=5 2gL
答:
(1)悬线与竖直方向夹角应为90°,才能使小球由静止释放后运动至最低点时,小球速度恰好为零.
(2)当细线与竖直方向成45°角时,至少要给小球一个
的速度,才能使小球做完整的圆周运动.5 2gL
