问题
选择题
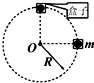
如图所示,质量为m的小球置于立方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,要使在最高点时盒子与小球之间作用力恰为mg,则( )
A.该盒子做匀速圆周运动的周期一定小于π2R g
B.该盒子做匀速圆周运动的周期一定等于π2R g
C.盒子在最低点时盒子与小球之间的作用力大小可能小于3mg
D.盒子在最低点时盒子与小球之间的作用力大小可能大于3mg
答案
AB、要使在最高点时盒子与小球之间恰好为mg,则盒子顶部对小球必然有向下的弹力mg,则有mg+mg=m
,解得该盒子做匀速圆周运动的速度v=v2 R
,该盒子做匀速圆周运动的周期为T=2gR
=π2πR v
,故A错误,B正确;2R g
CD、在最低点时,盒子与小球之间的作用力和小球重力的合力提供小球运动的向心力,由F-mg=m
,解得F=3mg,故C、D错误.v2 R
故选B.
