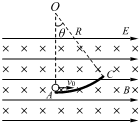
如图所示,某空间内存在着正交的匀强电场和匀强磁场,电场方向水平向右,磁场方向垂直于纸面向里.一段光滑绝缘的圆弧轨道AC固定在场中,圆弧所在平面与电场平行,圆弧的圆心为O,半径R=1.8m,连线OA在竖直方向上,圆弧所对应的圆心角θ=37°.现有一质量m=3.6×10-4kg、电荷量q=9.0×10-4C的带正电的小球(视为质点),以v0=4.0m/s的速度沿水平方向由A点射入圆弧轨道,一段时间后小球从C点离开圆弧轨道.小球离开圆弧轨道后在场中做匀速直线运动.不计空气阻力,sin37°=0.6,cos37°=0.8.求:
(1)匀强电场场强E的大小;
(2)小球刚射入圆弧轨道瞬间对轨道压力的大小.
(1)小球离开轨道后做匀速直线运动,其受力情况如图1所示,则有

qE=mgtanθ ①
所以 E=3.0N/C
(2)设小球运动到C点时的速度为v.在小球沿轨道从A运动到C的过程中,根据动能定理有qERsinθ-mgR(1-cosθ)=
mv2-1 2
mv02 ②1 2
解得 v=5.0m/s ③
小球由A点射入圆弧轨道瞬间,设小球对轨道的压力为N,小球的受力情况如图2所示,根据牛顿第二定律有N+qBv0-mg=
④mv02 R
根据图1还有:qvB=
⑤mg cosθ
由③④⑤可求得:N=3.2×10-3N
根据牛顿第三定律可知,小球由A点射入圆弧轨道瞬间对轨道的压力
N′=N=3.2×10-3N
答:
(1)匀强电场场强E的大小为3.0N/C;
(2)小球刚射入圆弧轨道瞬间对轨道压力的大小为3.2×10-3N.
