问题
问答题
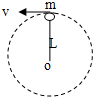
如图质量为m=0.2kg的小球固定在长为L=0.9m的轻杆一端,杆可绕O点的水平转轴在竖直平面内转动,g=10m/s2,求:
(1)小球在最高点的速度v1为多大时,球对杆的作用力为0?
(2)当小球在最高点的速度v2=6m/s时,球对杆的作用力和方向.
答案
小球在最高点时,对小球受力分析,受重力G和杆的弹力N,假定弹力N向下,如图所示;
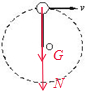
由牛顿第二定律和向心力公式得:N+G=
①mv2 r
(1)由①式解得N=0时的速度v1=
=gL
m/s=3m/s10×0.9
(2)由①式得小球在最高点的速度v2=6m/s时,杆对球的作用力为:N=
-mg=(mv2 r
-0.2×10)N=+6N0.2×62 0.9
“+“说明方向竖直向下
由牛顿第三定律得:球对杆的作用力大小 N′=N=6N,方向竖直向上.
答:球对杆的作用力为0时小球在最高点的速度为3m/s,当小球在最高点的速度v2=6m/s时,球对杆的作用力大小为6N,方向竖直向下.
