问题
问答题
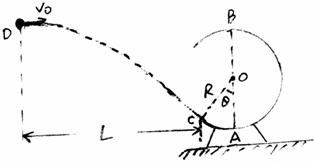
如图所示,一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内,轨道的一个端点C和圆心O的连线与竖直方向夹角θ=45°,A为轨道最低点,B为轨道最高点.一个质量m=0.50kg的小球从空中D点以V0=6m/s的速度水平抛出,恰好从轨道的C端沿切线方向进入轨道,重力加速度g=10m/s2,求:
(1)小球抛出点D距圆轨道C端的水平距离L.
(2)小球经过轨道最低点A时,受到轨道的作用力FA.
(3)判断小球能否到达最高点B,说明理由.
答案
(1)小球抛出后做平抛运动,小球恰好从轨道的C端沿切线方向进入轨道,说明小球的末速度应该沿着C点切线方向,
将平抛末速度进行分解,根据几何关系得:
C点速度在竖直方向的分量:vy=v0tan45°=6m/s
竖直方向的分运动为自由落体运动,t=
=0.6svy g
水平方向做平抛运动,L=v0t=3.6m
(2)由机械能守恒定律,有
mvC2+mg(R-Rcos45°)=1 2
mvA21 2
根据向心力公式得:
FA-mg=mvA2 R
解得:FA=43.9N
(3)设小球能到达B点,根据机械能守恒定律,有
mv02+mg(h-R-Rcos45°)=1 2
mvB21 2
解得:vB=
m/s>38 gR
所以可以到达B点.
答:(1)小球抛出点D距圆轨道C端的水平距离L为3.6m;
(2)小球经过轨道最低点A时,受到轨道的作用力FA为43.9N;
(3)小球能到达最高点B.
