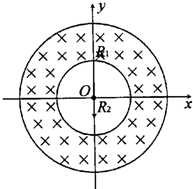
如图所示,在直角坐标系xOy决定的平面内,有两个同心圆,外侧圆半径为R1,内侧圆半径为R2,圆心为O.两圆之间的圆环内有磁感应强度为B的匀强磁场,磁场方向垂直于纸面指向纸内.在圆心O处有一质子源,沿y轴负方向发射质子流,质子流中质子的速度范围为0~v.结果有的质子从内侧圆离开磁场,有的质子从外侧圆离开磁场.已知质子带电量为e,质量为m,不考虑质子通过磁场后再进入磁场的情况.
(1)求所有质子通过的内侧圆的孤长;
(2)质子在磁场中运动的最长时间.
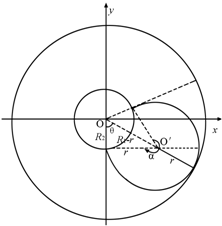
(1)由题意可知,轨迹圆与外侧圆相切时,对应的质子离开内侧圆的弧长最长,设圆半径为r,如图所示,由几何关系可得:
r2+
=(R1-r)2R 22
tanθ=r R2
联立以上两式解得:
θ=arctan(
)
-R 21 R 22 2R1R2
所以,所有质子通过的内侧圆的弧长:
L=2θ•R2
∴L=2R2arctan(
)
-R 21 R 22 2R1R2
(2)质子运动周期:
T=2πm eB
如图所示,质子从内侧圆离开对应的最大圆心角为:
α=2π-(π-2θ)=π+2θ
所以,质子从内侧圆离开的质子在磁场中运动的最长时间为:
tmax=T•
=mα 2π
.π+2arctan(
)
-R 21 R 22 2R1R2 eB
从外侧圆离开的质子速度更大,弧长更短,所以在磁场中运动的时间比tmax小,tmax即为质子在磁场中运动的最长时间.
答:(1)求所有质子通过的内侧圆的孤长为2R2arctan(
).
-R 21 R 22 2R1R2
(2)质子在磁场中运动的最长时间为m
.π+2arctan(
)
-R 21 R 22 2R1R2 eB
