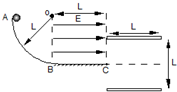
如图,一光滑轨道ABC,AB部分为半径为L的
圆周,水平部分BC 宽度为L,置于水平向右且大小为E的匀强电场中.一质量为m,电量q=1 4
的带正电小球(可视为质点)从A处静止释放,并从C处沿平行板电容器的中线射入.已知电容器板长L,两板距离为L,重力加速度g.mg 2E
(1)求小球经过圆弧B处轨道所受压力及小球到达C处的速度vc;
(2)当电容器两板间电压U=
,且上板电势高于下板时,求球在电容器中飞行时的加速度a以及飞离电容器时的偏转量y;mgL 2q
(3)若电容器电压U可变,要使小球能飞出电容器,求U的范围.(写主要过程)
(1)从A到B,由机械能守恒:mgL=
m1 2
…①v 2B
在B处,由向心力公式有:N-mg=m
…②v 2B L
解得:N=3mg
由牛顿第三定律,轨道所受压力N′=3mg,方向竖直向下
从A到C,由动能定理:mgL+qEL=
m1 2
…③v 2C
解得:vC=3gL
(2)由牛顿第二定律:mg+
=ma 得a=1.5g(向下)…④qU L
小球在电容器中飞行时间t=
…⑤L vC
飞离时偏转量y=
at2…⑥1 2
联立③~⑥得:y=
L 1 4
(3)由⑥知当y=
L时,有a=3g 1 2
当a向下,且上板电势高于下板时
有mg+
=ma 得U1=qU1 L
=4EL 2mgL q
当a向上,有上板电势低于下板
即
-mg=ma 得U2=qU2 L
=8EL4mgL q
即小球能飞出电容器,必须有:
当上板电势高于下板时,U<4EL
或者当上板电势低于下板时,U<8EL
答:(1)小球经过圆弧B处轨道所受压力为3mg,小球到达C处的速度为
;3gL
(2)当电容器两板间电压U=
,且上板电势高于下板时,球在电容器中飞行时的加速度a为1.5g,飞离电容器时的偏转量y为mgL 2q
L;1 4
(3)若电容器电压U可变,要使小球能飞出电容器,必须有:当上板电势高于下板时,U<4EL;或者当上板电势低于下板时,U<8EL.
