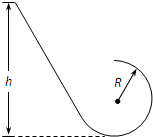
一质量m=2kg的小球从光滑斜面上高h=3.5m处由静止滑下,斜面底端紧接着一个半径R=1m的光滑圆环,如图所示,试求:(g=10m/s2)
(1)小球滑至圆环顶点时对环的压力;
(2)小球至少应从多高处由静止滑下才能越过圆环最高点;
(3)小球从h'=2m处由静止滑下时,脱离圆环的位置和圆心的连线与竖直方向夹角的余弦.
(1)设小球滑至环顶时的速度为υ1,所受环的压力为N.
小球运动过程中机械能守恒:mg(h-2R)=
m1 2
①υ 21
在顶点由圆周运动的知识有:mg+N=m
②υ 21 R
联立①②解得:N=mg(
-5)(2h R
代入数值解得:N =2×10(
-5)N=40N2×3.5 1
由牛顿第三定律知小球对环的压力大小为:N'=N=40N
(2)当圆环对小球的压力为零时,仅由重力充当向心力,对应的速度υ2为越过圆环最高点的最小速度,对应的高度h1为最低高度,由机械能守恒定律及圆周运动知识有:mg(h1-2R)=
m1 2
③υ 22
mg=m
④υ 22 R
联立③④解得:h1=
R=2.5m5 2
(3)由于h'<h1,故球在还没有到达顶端前即与环脱离,设脱离圆环时的位置半径与竖直方向的夹角为α,选轨道最低点为零势点,由机械能守恒定律及圆周运动知识有:mgh′=
mυ2+mgR(1+cosα)⑤1 2
mgcosα=m
⑥υ2 R
联立⑤⑥解得:cosα=
=2(h′-R) 3R 2 3
答:(1)小球滑至圆环顶点时对环的压力为40N.
(2)小球至少应从2.5m高处由静止滑下才能越过圆环最高点.
(3)小球从h'=2m处由静止滑下时,脱离圆环的位置和圆心的连线与竖直方向夹角的余弦为
.2 3
