如图所示,与水平面成37°的倾斜轨道AB,其延长线在C点与半圆轨道CD(轨道半径R=1m)相切,全部轨道为绝缘材料制成且放在竖直面内.整个空间存在水平向左的匀强电场,MN的右侧存在垂直纸面向里的匀强磁场.一个质量为0.4kg的带电小球沿斜面下滑,至B点时速度为VB=100/7 m/s,接着沿直线BC(此处无轨道)运动到达C处进入半圆轨道,进入时无动能损失,且刚好到达D点,从D点飞出时磁场消失,不计空气阻力,取g=10m/s2,cos37°=0.8,求:
(1)小球带何种电荷.
(2)小球离开D点后的运动轨迹与直线AC的交点距C点的距离.
(3)小球在半圆轨道部分克服摩擦力所做的功.
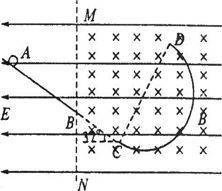
(1)由小球离开B点后仍能沿直线方向运动,则可确定电场力、与洛伦兹力的方向,从而可得出小球带正电.
(2)小球在BC间做匀速直线运动,则有C点的速度与B点的速度相等,即vc=
m/s 100 7
在BC段受力如图所示,设重力与电场力合力为F,
则有F=qvB,
又F=
=5N mg cos37°
解得:qB=
=F v 7 20
在D处由牛顿第二定律可得:BqvD+F=mv 2D R
由以上两式可得:vD=4m/s或vD=-
m/s(舍去)25 8
小球离开D点后做类平抛运动,其加速度为:由2R=
at2得:1 2
t=
=2×2R a
=4mR F
s2 2 5
s=vDt=2.26m
(3)设CD段克服摩擦力做功Wf,
由运动定理可得:-Wf-2FR=
m1 2 (v 2D
)-v 2C
解得Wf=27.6J.
