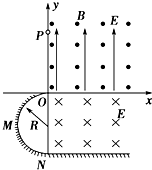
如图所示,竖直平面坐标系xOy的第一象限,有垂直:xOy面向外的水平勻强磁场和竖直向上的匀强电场,大小分别为B和E第四象限有垂直xOy為面向里的水平匀强电场,大小E'=2E 第三象限内有一绝缘光滑竖直放置的半径为R的半圆轨道,轨道最髙点与坐标原点O相切,最低点与绝缘光滑水平面相切于N.一质量为m的带电小球从y轴上(y>0)的P点沿工轴正方向进入第一象限后做圆周运动,恰好通过坐标原点O,且水平切入半圆轨道并沿轨道内侧运动,过N点水平进入第四象限,并在电场
中运动•(已知重力加速度为g)
(1)判断小球的带电性质并求出其所带电荷量.
(2)P点距坐标原点O至少多高?
(3)若该小球以满足(2)中OP最小值的位置和对应速度进入第一象限,通过N点开始计时,经时间t=2
,小球距N点的距离s为多远?R g
(1)小球进入第一象限正交的电场和磁场后,在垂直磁场的平面内做圆周运动,说明重力与电场力平衡,qE=mg ①
得q=
②mg E
小球带正电.
(2)小球在洛伦兹力作用下做匀速圆周运动,设匀速圆周运动的速度为v、轨道半径为r.
有:qvB=m
③v2 r
小球恰能通过半圆轨道的最高点并沿轨道运动,有:mg=m
④v2 R
由③④得:r=
⑤m gR Bq
PO的最小距离为:y=2r=2
⑥m gR Bq
(3)小球由O运动到N的过程中机械能守恒:mg•2R+
mv2=1 2 1 2
⑦mv 2N
由④⑦得:vN=
=4Rg+v2
⑧5gR
根据运动的独立性可知,小球从N点进入电场区域后,在x轴方向以速度vN做匀速直线运动,沿电场方向做初速度为零的匀加速直线运动,则沿x轴方向有:x=vNt⑨
沿电场方向有:y=
at2⑩1 2
a=
=qE′ m
=2g⑪2qE m
t时刻小球距N点:s=
=6Rx2+d2
