问题
填空题
设p:(4x-3)2-1≤0,q:x2-(2m+1)x+m(m+1)≤0,若¬p是¬q的必要不充分条件,则实数m的取值范围是______.
答案
由:(4x-3)2-1≤0,得-1≤4x-3≤1,
解得
≤x≤1,即p:1 2
≤x≤1.1 2
由x2-(2m+1)x+m(m+1)≤0,
得(x-m)(x-m-1)≤0,
即m≤x≤m+1,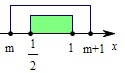
∴q:m≤x≤m+1.
∵¬p是¬q的必要不充分条件,
∴q是p的必要不充分条件.
即
,m≤ 1 2 m+1≥1
解得0≤m≤
,1 2
即实数m的取值范围是[0,
].1 2
故答案为:[0,
].1 2
