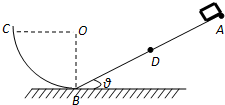
如图所示,倾角θ=30°、长L=2.7m的斜面,底端与一个光滑的1/4圆弧平滑连接,圆弧底端切线水平.一个质量为m=1kg的质点从斜面最高点A沿斜面下滑,经过斜面底端B恰好到达圆弧最高点C,又从圆弧滑回,能上升到斜面上的D点,再由D点由斜面下滑沿圆弧上升,再滑回,这样往复运动,最后停在B点.已知质点与斜面间的动摩擦因数为μ=
/6,g=10m/s2,假设质点经过斜面与圆弧平滑连接处速率不变.求:3
(1)质点第1次经过B点时对圆弧轨道的压力;
(2)质点从A到D的过程中质点下降的高度;
(3)质点从开始到第6次经过B点的过程中因与斜面摩擦而产生的热量.
(1)设圆弧的半径为R,则质点从C到B过程,由mgR=
mυ21 2 FN-mg=m υ2 R
得:FN=3mg=3×1×10N=30N
根据牛顿第三定律,质点第1次经过B点对圆弧轨道的压力为30N.
(2)设质点第一次由B点沿斜面上滑的速度为υ1,B点到D点的距离为L1mgLsin30o-μmgcos30oL=
m1 2 υ 21 -mgL1sin30o-μmgcos30oL1=0-
m1 2 υ 21
代入数据解得:L1=
L=0.9m 1 3
则质点从A点到D点下降的高度h=0.9m
(3)设质点第2次由B点沿斜面上滑的速度为υ2,沿斜面上滑的距离为L2.则mgL1sin30o-μmgcos30oL1=
m1 2 υ 22 -mgL2sin30o-μmgcos30oL2=0-
m1 2 υ 22
得:L2=
L11 3
同理可推得:质点第n次由B点沿斜面上滑的距离Ln为Ln=
Ln-1=(1 3
)nL1 3
所以质点从开始到第6次经过B点的过程中,在斜面上通过的路程为
S=L+2(L1+L2)=5.1m
Q=μmgcos30°S=12.75J
答:(1)质点第1次经过B点时对圆弧轨道的压力为30N.
(2)质点从A到D的过程中质点下降的高度为0.9m.
(3)质点从开始到第6次经过B点的过程中因与斜面摩擦而产生的热量为12.75J.
