问题
问答题
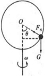
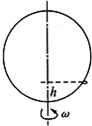
一个小圆环套在置于竖直面内半径为R的大圆环上,并能沿大圆环无摩擦地滑动,当大圆环绕一个穿过其中心的竖直轴转动时,小圆环便相对静止在距大圆环最低点上方h处,如图所示,试求:
(1)小圆环做圆周运动的半径r
(2)大圆环转动的角速度
答案
(1)由几何关系知,小环做圆周运动的半径为:r=
=R2-(R-h)2
.2Rh-h2
(2)如图所示,小环受重力和支持力,两个力的合力提供向心力,有:
F合=mgtanθ=mRsinθω2,
解得:ω=
=g Rcosθ
.g R-h
答:(1)小圆环做圆周运动的半径r=
;2Rh-h2
(2)大圆环转动的角速度为
.g R-h