方程至少有一正根的充要条件是a＞-1

方法一 若a=0，则方程变为-x+1=0,x=1满足条件，若a≠0，则方程至少有一个正根等价于



或-1＜a＜0或a＞0.

综上：方程至少有一正根的充要条件是a＞-1.

方法二 若a=0，则方程即为-x+1=0,

∴x=1满足条件；若a≠0，∵Δ=(a²+a+1)²-4a(a+1)=(a²+a)²+2(a²+a)+1-4a(a+1)

=(a²+a)²-2a(a+1)+1=(a²+a-1)²≥0，∴方程一定有两个实根.

故而当方程没有正根时，应有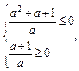解得a≤-1,

∴至少有一正根时应满足a＞-1且a≠0,

综上：方程有一正根的充要条件是a＞-1.