问题
解答题
证明一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac＜0.
答案
充分性：若ac＜0,则b2-4ac＞0,且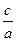
＜0,
∴方程ax2+bx+c=0有两个相异实根，且两根异号，即方程有一正根和一负根.
必要性：若一元二次方程ax2+bx+c=0有一正根和一负根，则Δ=b2-4ac＞0,x1x2=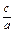
＜0,∴ac＜0.
综上所述，一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac＜0.
充分性：若ac＜0,则b2-4ac＞0,且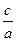＜0,
∴方程ax2+bx+c=0有两个相异实根，且两根异号，即方程有一正根和一负根.
必要性：若一元二次方程ax2+bx+c=0有一正根和一负根，则Δ=b2-4ac＞0,x1x2=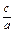＜0,∴ac＜0.
综上所述，一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac＜0.