如图所示，在光滑的圆锥顶端，用长为L=2m的细绳悬一质量为m=1kg

问题问答题

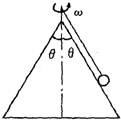
如图所示，在光滑的圆锥顶端，用长为L=2m的细绳悬一质量为m=1kg的小球，圆锥顶角为2θ=74°．求：

（1）当小球ω=1rad/s的角速度随圆锥体做匀速圆周运动时，细绳上的拉力．

（2）当小球以ω=5rad/s的角速度随圆锥体做匀速圆周运动时，细绳上的拉力．

答案

（1）小球刚要离开锥面时的速度，此时支持力为零，根据牛顿第二定律得：

mgtanθ=mω02Lsinθ

解得：ω₀=2.5rad/s，

当ω=1rad/s＜2.5rad/s时，小球没有离开斜面，

根据牛顿第二定律得：

Tsinθ-Ncosθ=mω²Lsinθ

Tcosθ+Nsinθ=mg

带入数据得：

T-

T+

N=10

解得：T=8.72N

（2）当ω=5rad/s＞2.5rad/s时，小球离开锥面，设细线与竖直方向夹角为β

T₁sinβ=mω²Lsinβ

解得：T₁=mω²L=1×25×2=50N

答：（1）当小球ω=1rad/s的角速度随圆锥体做匀速圆周运动时，细绳上的拉力为8.72N．

（2）当小球以ω=5rad/s的角速度随圆锥体做匀速圆周运动时，细绳上的拉力为50N．